KMP字符串匹配

模板&原理

记border:既是的前缀又是的后缀，且长度小于的字符串为的border next数组：next[i]=s[1,2,,i]的最长border长度。

对于一个字符串的匹配，最容易想到的是从头开始逐个判断，但是这样的时间复杂度就远超预期了，而通过标记的next数组，我们可以减少一定不能成立的情况。

---

模板题：P3375 【模板】KMP字符串匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

给出两个字符串 和 ，若 的区间 子串与 完全相同，则称 在 中出现了，其出现位置为 。
现在请你求出 在 中所有出现的位置。

定义一个字符串 的 border 为 的一个非 本身的子串 ，满足 既是 的前缀，又是 的后缀。
对于 ，你还需要求出对于其每个前缀 的最长 border 的长度。

输入格式

第一行为一个字符串，即为 。
第二行为一个字符串，即为 。

输出格式

首先输出若干行，每行一个整数，按从小到大的顺序输出 在 中出现的位置。
最后一行输出 个整数，第 个整数表示 的长度为 的前缀的最长 border 长度。

样例 #1

样例输入 #1

ABABABC
ABA

样例输出 #1

1
3
0 0 1

提示

样例 1 解释

。

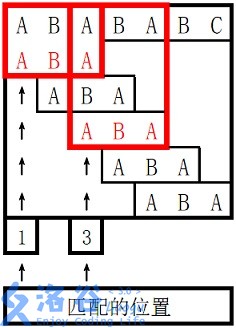对于 长度为 的前缀 ABA，字符串 A 既是其后缀也是其前缀，且是最长的，因此最长 border 长度为 。

数据规模与约定

本题采用多测试点捆绑测试，共有 3 个子任务。

• Subtask 1（30 points）：，。
• Subtask 2（40 points）：，。
• Subtask 3（30 points）：无特殊约定。

对于全部的测试点，保证 ， 中均只含大写英文字母。

题解

这里的提示图十分清楚，红色框的情况才是我们需要检测是否匹配的。而真正有思维难度的不是知道next数组后对数组的检测，而是如何得到next数组，这里借助样例来解释。

首先对需要匹配的字符串进行预处理。

预处理

只有结尾处的后缀与前缀相同，且相同的最大长度为1。这里要注意的是判断border最大长度时要忽略自身（第一个元素）否则会进入死循环。

于是上述提示红色框的取法是不是就有些眉目了呢。上面给出的是找到全部匹配的情况，这里再给出只有部分匹配的情况（与题目不同）。

部分匹配

这里到B之后就不匹配了，那么由于next[2]=0即border的最大长度为零，我们就从B的下一个开始继续检测。

下一步

于是KMP的完整逻辑就完成了。

代码如下：

#include<stdio.h>  
#include<string.h>  
char s1[1000006];  
char s2[1000006];  
int next[1000006];  
int main()  
{  
    scanf("%s%s",s1+1,s2+1);  //让数组的下标从1开始
    int n=strlen(s1+1),m=strlen(s2+1);  
    int j=0;  
    for(int i=2;i<=m;i++){  //从2开始，忽略第一个数
        while(j&&s2[i]!=s2[j+1])j=p[j];  //从最大border处开始
        if(s2[i]==s2[j+1])j++;  //逐个检测，排除j=0
        next[i]=j;  //记录next数组
    }  
    j=0;  
    for(int i=1;i<=n;i++){  
        while(j&&s1[i]!=s2[j+1])j=next[j];  
        if(s1[i]==s2[j+1])j++;  
        if(j==m){  
            printf("%d\n",i-m+1);  
            j=next[j];  
        }  
    }  
    for(int i=1;i<=m;i++)printf("%d ",next[i]);  
    return 0;  
}

---

应用

题目1：P4391 [BOI2009]Radio Transmission 无线传输 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

题目描述

给你一个字符串 ，它是由某个字符串 不断自我连接形成的。但是字符串 是不确定的，现在只想知道它的最短长度是多少。

输入格式

第一行一个整数 ，表示给出字符串的长度。

第二行给出字符串 的一个子串，全由小写字母组成。

输出格式

仅一行，表示 的最短长度。

样例 #1

样例输入 #1

8
cabcabca

样例输出 #1

3

提示

样例输入输出 1 解释

对于样例，我们可以利用 不断自我连接得到 ，读入的 ，是它的子串。

规模与约定

对于全部的测试点，保证 。

解析

对于这个我们可以从最后的位置入手，因为最后一次一定要输出结尾，所以对于最短的长度即是总能长度减去最后一个数的最大border。 如果给出字符串是没有循环的：

没有循环

字符串有循环：

有循环

代码如下：

#include<stdio.h>
#include<string.h>
char s2[1000006];
int p[1000006];
int main()
{
    int m;
    scanf("%d%s",&m,s2+1);
    int j=0;
    for(int i=2;i<=m;i++){
        while(j&&s2[i]!=s2[j+1])j=p[j];
        if(s2[i]==s2[j+1])j++;
        p[i]=j;
    }
    printf("%d",m-p[m]);
    return 0;
}